A13 ЕГЭ (повышенный уровень, время – 6 мин)
Тема: Выполнение алгоритмов для исполнителя.
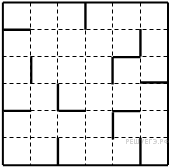
Пример 1 A13 Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо

При выполнении этих команд РОБОТ перемещается на одну клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия стены у той клетки, где находится РОБОТ:
Сверху свободно
Снизу свободно
Слева свободно
Справа свободно
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?
НАЧАЛО
ПОКА <слева свободно> вниз
ПОКА <снизу свободно> вправо
ПОКА <справа свободно> вверх
ПОКА <сверху свободно> влево
КОНЕЦ
1) 1 2) 2 3) 3 4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в той же клетке, с которой он начал движение.
Так как программа заканчивается командой "ПОКА <сверху свободно> влево", следовательно для того, чтобы робот остановился в той же клетке, с которой он начал движение, необходимо, чтобы у этой клетки была стенка сверху.
Этому условию удовлетворяют все клетки верхней стенки лабиринта и еще шесть клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию 1. Обратим внимание, что возможны зацикливания, например, если начать движение из клетки А1, Б1, если нумеровать цифрами сверху вниз, а буквами слева направо.
Ответ: три клетки В1, А2 и Д3.
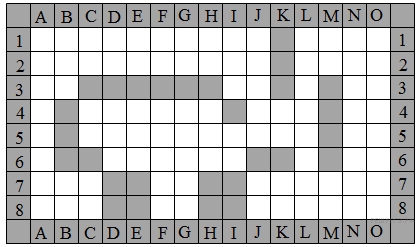
Пример 2 A13 Исполнитель МАШИНКА «живет» в ограниченном прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке. Серые клетки – возведенные стены, светлые – свободные клетки, по которым МАШИНКА может свободно передвигаться. По краю поля лабиринта также стоит возведенная стенка с нанесенными номерами и буквами для идентификации клеток в лабиринте.

Система команд исполнителя МАШИНКА:
вверх вниз влево вправо
При выполнении любой из этих команд МАШИНКА перемещается на одну клетку соответственно (по отношению к наблюдателю): вверх ↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится МАШИНКА (также по отношению к наблюдателю):
сверху
свободно снизу
свободно слева
свободно справа
свободно
Цикл
ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, стартовав в ней и выполнив предложенную ниже программу, МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно> вниз
ПОКА <справа свободно> вправо
вверх
вправо
КОНЕЦ
1) 10
2) 14
3) 3
4) 22
Решение
Начав движение из любой клетки столбца А, клеток В7, 8 С7, 8 Машинка разобьется.
Начав движение из клеток В1-В3, Машинка уцелеет.= > +3 клетки.
Начав движение из любой клетки первых двух строк, начиная со столбца С и до столбца I, Машинка разобьется.
Начав движение из любой клетки столбца J, Машинка разобьется.
Начав движение из любой клетки столбца K, L, M, N Машинка разобьется.
Проанализировав "пещеру" (участок лабиринта в центре, из которого только один выход), приходим к выводу, что Машинка Не разобьется, стартовав из столбцов D и E, H, I. В каждом из них по три клетки, а в столбце I 2. Следовательно, ответ 3 + 9 + 2 = 14.
Пример 3 A13 Исследуя записи в тетради одного из пиратов, кладоискатели обнаружили следующие указания:
1.60 шагов на юг
2.30 шагов на восток
3.30 шагов на север
4.60 шагов на юг
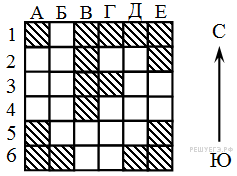
Предположительно, этому алгоритму должен следовать человек, желающий найти закопанный клад. Продолжив свои исследования, кладоискатели обнаружили также и карту острова, на котором должен располагаться тайник с кладом (см. рис.). Сторона каждого квадрата на этой карте приблизительно равна 30 шагам. Заштрихованный квадрат означает непроходимую местность (например, море), белый квадрат – проходимые участки суши.

Самое обидное то, что на карте не обозначено место, в котором должен стоять кладоискатель перед началом выполнения указанной выше последовательности действий. Однако, учитывая неправильную форму острова, кладоискатели пришли к выводу, что такое место можно однозначно определить, используя алгоритм. Укажите, в центре какого квадрата, согласно имеющейся информации, должен находиться клад.
1) A4
2) E4
3) Г6
4) Б5
Решение.
1. 60 шагов на юг (2 клетки) можно сделать только из 7 клеток.
2. Потом нужно сделать 30 шагов на восток, следовательно, клетки, из которых после команды 1 нельзя сделать 30 шагов на восток нам не подходят (весь ряд Б, кроме Б3, Г4, Д3, Д4 и Е)
3. Проверив оставшиеся клетки, понимаем, что это клетка, в которую мы попадем, стартуя из А2, то есть Б5